Mathesis Pesaro       mathesispesaro.altervista.org

 

 

 

Triangoli con un vertice mobile

L'esempio che presentiamo si riferisce alla strutturazione dell'insieme dei triangoli. Questo argomento può essere affrontato, a livelli diversi di complessità e approfondimento, a partire dal secondo ciclo della scuola elementare fino al biennio delle superiori. L'analisi che segue riguarda uno solamente dei tanti modelli che possono essere utilizzati a questo scopo; del modello preso in esame indichiamo le modalità di costruzione e, in maniera sintetica, tutte le indagini possibili su di esso (Guida all'analisi).
Il sapere matematico esposto in dettaglio, fa invece riferimento alle domande delle sezioni "Figure" e "Lati".
Per il quadro teorico di riferimento relativo a questo approccio didattico e le modalità concrete dell'operare (organizzazione del lavoro e gestione delle attività della classe), sia dal punto di vista dell'alunno che dell'insegnante, rimandiamo a pubblicazioni

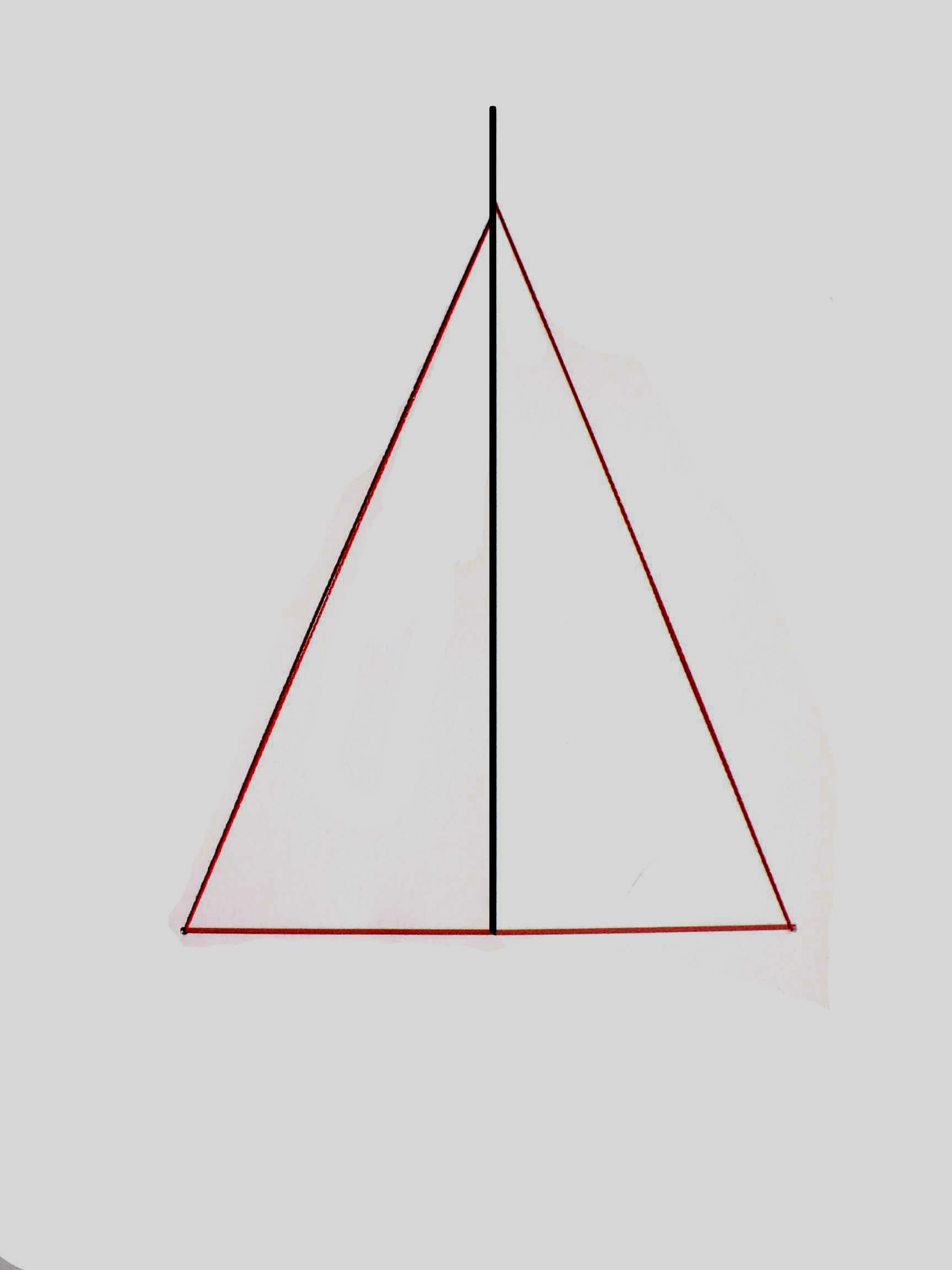
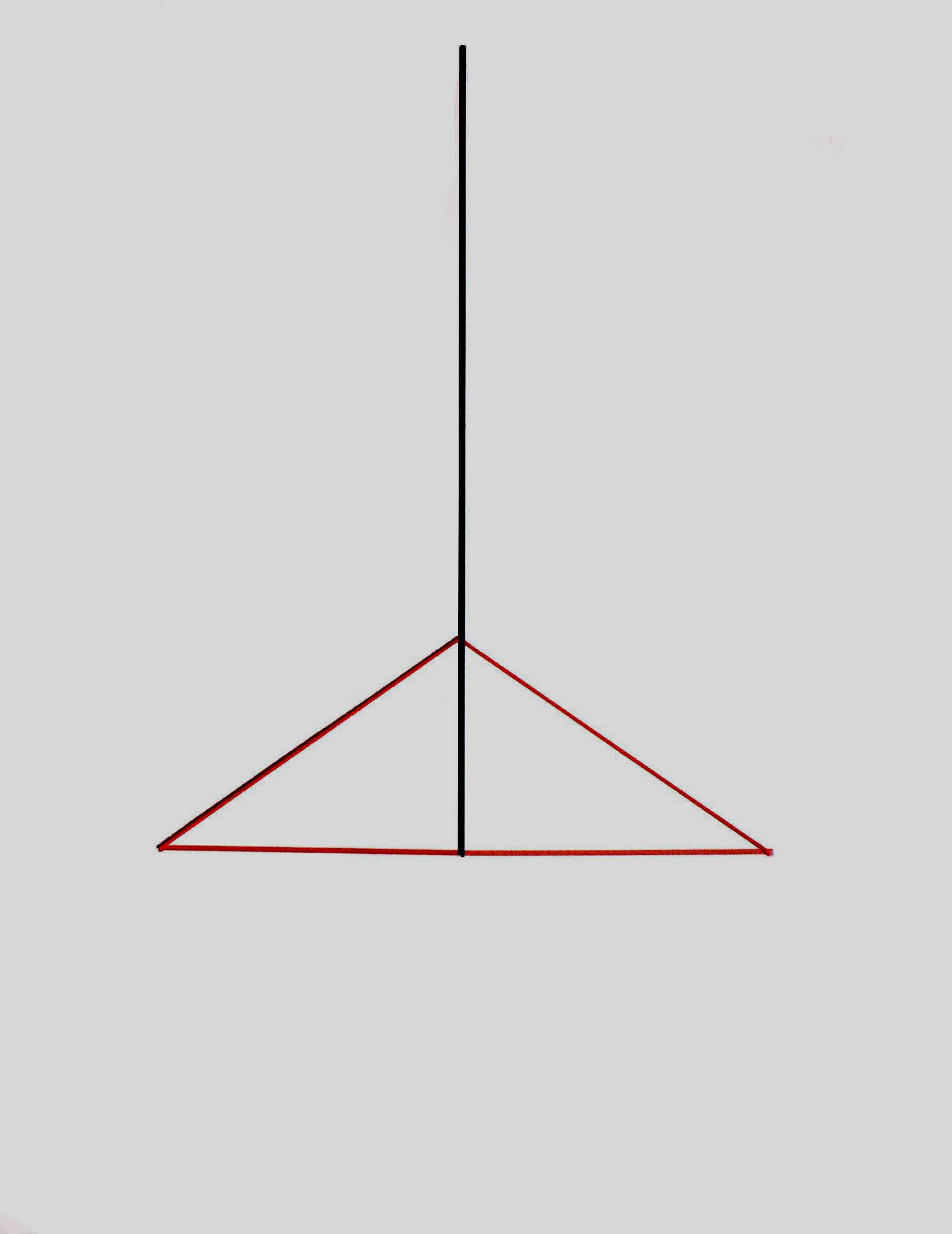
Costruzione del modello

Guida all’analisi

Trasla il vertice mobile nella scanalatura e rispondi alle seguenti domande.

Figure

  • Quali e quanti triangoli si formano?
  • Trasla il vertice mobile fino a sovrapporlo al lato AB, descrivi la figura che si ottiene.
  • Immagina di poter proseguire la traslazione oltre il modello. Esiste un punto oltre il quale la traslazione non è più possibile? Perché?

Lati
  • Modificano le loro misure? Esamina la situazione considerando i due versi di traslazione.
  • Confronta in più casi la misura dei lati variabili. Che cosa osservi?
  • C’è un triangolo che presenta una particolarità rispetto ai lati? Quale?
  • Cosa ti suggerisce la presenza di questo particolare triangolo?
  • Rappresenta la situazione con un diagramma di Venn
  • Prova ora a definire l’insieme dei triangoli che il modello genera considerando la proprietà che hai scoperto.

Angoli
  •  Modificano la loro misura? Esamina la situazione considerando i due versi di traslazione.
  • Confronta in più casi la misura degli angoli alla base. Cosa noti?
  • Esiste una posizione in cui tutti gli angoli sono congruenti? Quale?
  • Prova ora a definire l’insieme dei triangoli che il modello genera considerando la proprietà che hai scoperto
  • Partendo dalla posizione in cui C è sulla base, trasla il vertice mobile e descrivi cosa accade all’angolo al vertice.
  • Qual è la misura degli angoli alla base e dell’angolo al vertice nei due casi limite? Cosa ti suggerisce questo fatto?
  • Quando un angolo aumenta cosa accade al lato che gli sta di fronte? Cosa ti suggerisce questo fatto?
  • Quale relazione lega i tre angoli? Esprimila con linguaggio verbale e simbolico.
Area e perimetro
  • Nel movimento l’area si modifica? E il perimetro? Analizza la situazione considerando i due versi di traslazione.
  • Esistono posizioni di massimo e minimo per area e perimetro? Se sì, descrivile?
  • Quale relazione lega la misura dei lati variabili al perimetro? Esprimila con linguaggio verbale e simbolico.
  • Quale relazione lega l’altezza, riferita al lato fisso, e l’area? Esprimila con linguaggio verbale e simbolico.
Assi e centro di simmetria
I triangoli che il modello genera possiedono assi di simmetria? E centro di simmetria?
Se la tua risposta affermativa descrivi quali e quanti sono gli assi di simmetria e dove è situato il centro.

Ampliamento del modello 
Che cosa accade se l’incisione prosegue oltre la base? Progetta e costruisci il modello relativo. 
Fra gli infiniti triangoli che si formano, ne esistono di congruenti. Quanti? In quali posizioni?
Quale isometria li fa corrispondere?
Quale quadrilatero si ottiene considerando una qualsiasi coppia di triangoli congruenti?

Triangoli non ottenibili
 Esistono triangoli che il modello non può generare, ma che hai già incontrato utilizzando i legnetti incernierati. Quali? Perché?
Prova a progettare e a costruire un modello analogo a quello che hai esaminato, ma che nel movimento consenta di ottenere anche questo tipo di triangoli.

Sapere matematico

Figure generate dal modello e casi limite
Si formano infiniti triangoli isosceli di cui uno equilatero.

ll modello presenta una posizione limite, quella in cui il vertice C appartiene alla base; il triangolo è degenerato in segmenti sovrapposti. Traslando il vertice nel verso opposto il modello indica una nuova posizione limite quella in cui C è arrivato all’altra estremità della scanalatura.  E’ però possibile superare i limiti fisici del modello e pensare di poter traslare il vertice all’infinito e pertanto è all’infinito che troveremo l’altro caso limite. 

Lati
Un lato non modifica mai la sua misura, gli altri due diminuiscono quando il vertice mobile viene traslato verso la base e aumentano se la traslazione avviene nel verso opposto.
Rimane costante il rapporto tra le misure dei lati variabili che è sempre 1:1. In una particolare posizione tutti i lati sono congruenti. Gli infiniti triangoli generati dal modello hanno quindi sempre almeno due lati congruenti. E’ questa costante che ci consente di individuare l’insieme di cui si tratta, di definire le figure che si formano e di stabilire la relazione di inclusione tra insiemi.

Definizione - Triangoli isosceli: poligoni a tre lati di cui almeno due sono congruenti.

Il quantificatore almeno consente di includere nell’insieme considerato anche i triangoli equilateri.

Definizione -Triangoli equilateri: triangoli con tutti e tre i lati congruenti

Il grafico di Eulero-Venn visualizza la relazione di inclusione

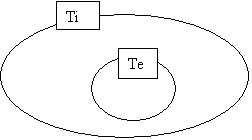
L’insieme dei Triangoli equilateri (Te)

è contenuto in quello dei triangoli isosceli (Ti).

Te  Ti





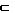© COPYRIGHT 2007 tutti i diritti riservati